Поезд харьков кривой рог расписание цена билета 2017: расписание поездов, жд билеты на поезд

Содержание

Дешевые рейсы из Кривой Рог в Харьков, сравнивайте и бронируйте легко

Харьков (или Харьков) — второй по величине город в Украине. Город, расположенный на северо-востоке страны, имеет очень большое население. Площадь Свободы, которая входит в число крупнейших городских площадей Европы, также является центром Харькова, который является крупным промышленным и культурным центром. Харьковский международный аэропорт встречает пассажиров, желающих посетить этот город.

Харьков имеет широкую транспортную сеть благодаря автомобильным и железным дорогам. На метро можно добраться до центральных частей города, а общественный транспорт, такой как автобусы, трамваи, троллейбусы, маршрутки и поезда, обеспечивает транспортные услуги в места, куда метро не доходит. Хотя услуги предоставляются с 5 утра до полуночи, у вас могут возникнуть трудности с поиском общественного транспорта в некоторые районы города после 9 часов.вечера.

Помимо городского транспорта, поезда и автобусы также обеспечивают транспортировку в соседние города. В некоторых районах города есть точки бесплатного Wi-Fi. Если на вашем телефоне нет доступа в интернет, вы можете легко узнать время работы этих услуг в этих точках. Если вам трудно найти дорогу, вы можете попросить помощи у билетных касс. Пожалуйста, не забудьте сохранить билет во время поездки. В противном случае вам, возможно, придется заплатить штраф в случае контроля билетов.

Полезно напомнить, что некоторые услуги тарифицируются выше в зависимости от расстояния. Помимо всего этого, вы можете предпочесть такси или прокат автомобилей для городского транспорта, чтобы воспользоваться более практичным вариантом добраться туда, куда вы хотите. Харьковский международный аэропорт находится в 12,5 км к юго-западу от города. Существуют различные варианты транспорта из аэропорта в центр города. Тем не менее, в некоторые районы города может быть невозможно сразу добраться на общественном транспорте. Возможно, вам придется пересесть на автобус, троллейбус или микроавтобус. Вы также можете воспользоваться такси или арендовать автомобиль в аэропорту.

Автобус

Автобус № 115 отправляется из аэропорта до станции метро «Проспект Гагарина», а автобус № 119 идет до остановки «Победы». Автобус играет важную роль в городском транспорте. Есть много автобусных маршрутов, которые ходят по всему городу. На автобусе можно добраться практически в любую часть города.

Троллейбус

Доехать до остановок у кинотеатра «Зірка», ул. Кузнечной или ул. По городу курсирует около 30 троллейбусных маршрутов.

Микроавтобус

Транспортные средства, известные в Украине как маршрутки, представляют собой микроавтобусы, используемые в качестве вспомогательных линий городского транспорта. Маршрутки 225 и 152 отправляются из аэропорта до станции метро «Академика Барабашова».

Трамвай

Трамвай также является одним из наиболее популярных вариантов городского транспорта. В городе около 20 трамвайных линий. Трамваи есть практически на всех улицах Харькова. Трамвайные линии 2 и 15 отправляются от площади Свободы. Прямого трамвая из аэропорта нет. Однако, если вы приехали в любую часть города из аэропорта на троллейбусе, трамвае или автобусе, вы можете предпочесть трамвай в качестве варианта пересадки.

Метро

После прибытия в аэропорт вам нужно сесть на автобусы 115 или 119, чтобы добраться до станции метро. Доехав до станции метро «Проспект Гагарина», можно отправиться в любую часть города, воспользовавшись возможностью пересадок между линиями метро, либо сесть на маршрутки, отправляющиеся из аэропорта, и прибыть на станцию метро «Академика Барабашова». Метро отправляется каждые 2-3 минуты в часы пик, а в остальное время каждые 5-10 минут. Самая длинная линия метро – около 45 минут. Таким образом, вы можете добраться куда угодно на метро за очень короткое время. Вам нужно купить синие жетоны в автоматах возле станции, чтобы попасть в метро.

В Харькове есть три линии метро: Холодногорско-Заводская, Салтовская и Алексеевская. Линия 1, также известная как красная, проходит между станциями Холодная гора и Пролетарская.

С красной линии на синюю можно пересесть на станции Центральный рынок и на зеленую на станции Завод им. Станция Малышева.

Линия 2, также известная как синяя линия, проходит между станциями Центральный Рынок и Героев Труда. На красную ветку можно пересесть с синей ветки на первой станции и на зеленую ветку на станции Университет-Госпром.

Маршрут 3, известный как зеленая линия, проходит между Заводом им. Станции Малышева и Проспект Победы. На первой станции зеленой ветки можно пересесть на красную ветку, а на синюю ветку можно пересесть на станции «Университет-Госпром».

Электричка

Харьков-Пассажирский — центральный железнодорожный вокзал Харькова, расположенный недалеко от площади Свободы. Южный вокзал, расположенный на линии красной линии, связан с центральным железнодорожным вокзалом. Поезд чаще всего предпочитают для поездок в соседние города, а не городской транспорт. Хотя поезда медленнее по сравнению с Европой в целом, цены очень доступные.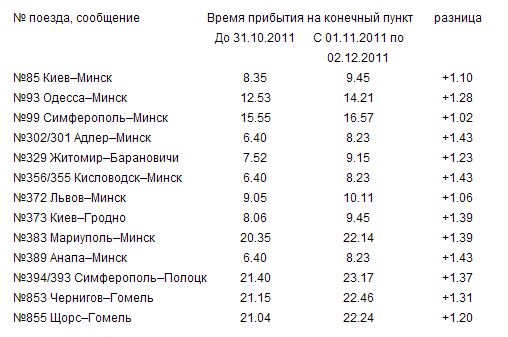

Такси

В Харькове вы можете быстрее добраться до места назначения на такси. Прибыв в аэропорт, вы можете взять такси на стоянке такси прямо возле здания аэропорта. Также в городе есть различные стоянки такси. Качество услуг варьируется в зависимости от компаний, предоставляющих эту услугу, а также стоимость проезда может различаться равномерно.

Прокат автомобилей

Вы можете воспользоваться услугой проката автомобилей в компании Rent A Car в здании Харьковского международного аэропорта. Так вы сможете свободно и с комфортом передвигаться по городу. Вы также можете арендовать автомобиль, когда доберетесь до центра города, а также можете забронировать автомобиль заранее, воспользовавшись опцией онлайн-бронирования.

Последнее обновление: 26 марта 2017 г.

Оптимизация стоимости проезда на высокоскоростной железной дороге Китая на основе поведения пассажиров

На этой странице Коэффициент загрузки и доход от HSR все еще можно улучшить за счет оптимизации структуры тарифов на билеты. В отличие от нынешней единой и неизменной структуры тарифов, в этом документе исследуется применение многоуровневых тарифов в HSR Китая. Исходя из того, что для каждого пункта отправления-назначения (O-D) одновременно может предлагаться только один класс тарифа, в этом документе рассматриваются вопросы о том, как со временем корректировать цену билета, чтобы максимизировать доход. Во-первых, на основе стратегии кусочного ценообразования строится модель оптимизации стоимости билета, которая может быть преобразована в решаемую выпуклую программу. Затем, на основе анализа регулярности прибытия пассажиров с использованием исторических данных о билетах линии Пекин-Шанхай ВСМ, проводится несколько экспериментов с использованием предложенного в статье метода для изучения свойств оптимальной схемы многоуровневого тарифа.

1. Введение

1.1. История исследований

Конкуренция между железнодорожными пассажирскими перевозками и другими видами пассажирских перевозок становится все более жесткой. В этой ситуации нынешняя единая и неизменная структура тарифов постепенно становится препятствием для увеличения доходов железной дороги и развития железнодорожной системы. Статистические данные, предоставленные компанией Пекин-Шанхайская высокоскоростная железная дорога (ВСМ) за 2014 год, показывают, что 13 процентов поездов имели коэффициент загрузки менее 65 процентов. Теоретически и на практике было подтверждено, что скидка на предварительную покупку, основанная на неопределенности и оценке спроса на поездки, может помочь в достижении эффективного распределения пропускной способности [1]. Следовательно, по сравнению с единой и неизменной структурой тарифа, многоуровневая структура тарифа может увеличить коэффициент использования ресурсов, в результате чего улучшится доход железнодорожной компании.

В этой статье предлагается многоуровневая структура тарифа для высокоскоростной железной дороги Китая. Исходя из того, что для каждой пары пунктов отправления и назначения (O-D) одновременно может быть предложен только один класс тарифа, в этой статье рассматривается, как корректировать цену билета с течением времени на основе поведения пассажиров при выборе для каждого O-D.

1.2. Обзор литературы

В ряде предыдущих работ были рассмотрены аспекты проблемы динамического ценообразования. Кинкейд и Дарлинг (1963) [2] заложили основу для изучения всесортной цены, построив две модели оптимизации для генерации оптимальных цен каждый раз с учетом того, объявлена ли цена. Гальего и ван Ризин (1994) [3] проанализировали структурные характеристики оптимальной цены на единичный продукт, доказав, что оптимальное решение детерминированной задачи является верхней границей стохастической задачи. На этой основе Гальего и Ван Райзин (1997) [4] нашли верхнюю границу оптимального ожидаемого дохода, анализируя детерминированную версию проблемы для нескольких продуктов.

Ценообразование относится к тактической проблеме. На практическом уровне необходимы методы для динамического определения оптимального времени изменения цен. Для уникального изменения цены разрешено быть выше или ниже, Фэн и Гальего (1995) [5] выдвинули стратегию контроля, основанную на временном пороге, зависящем от количества непроданных товаров. На основе этой работы Feng and Xiao (2000) [6] расширили подход, позволив множественные изменения цен. В дальнейшей работе Feng and Xiao (2000) [7] допустили обратное изменение заданных цен.

Исследование динамического ценообразования началось поздно в Китае, где цены на билеты традиционно оставались неизменными на протяжении десятилетий. С практической точки зрения Ши [8] преобразовал оптимальное решение в допустимое приближенное оптимальное решение. Чжан [9] применил теорию максимального вогнутого конверта для определения оптимальной скидки на проезд для каждого O-D поезда. С применением динамической теории игр Сюй и др. [10] установили динамическую модель ценообразования между HSR и авиаперевозками. Яо и др. [11] проанализировали стратегию ценообразования на ВСМ в коридоре Ухань-Гуанчжоу с учетом конкуренции между пассажирскими железнодорожными перевозками и другими видами транспорта. Bingyi [12] разработал модель динамического программирования для решения проблемы оптимизации доходов HSR с несколькими поездами, несколькими сегментами и несколькими классами, учитывая поведение пассажиров при выборе. Вэй и др. [13] построили двухуровневую модель программирования для задачи оптимизации стоимости проезда на высокоскоростных поездах с учетом преимуществ как железнодорожной единицы, так и пассажиров. На основе данных о работе высокоскоростной железной дороги Ли и Фу [14] изучили эластичность спроса, что является ключевой проблемой при оптимизации стоимости проезда. Чжэн и Лю [15] исследовали применение многоуровневого тарифа на высокоскоростной железной дороге Китая, при котором цены устанавливаются отдельно по O-D и по периоду времени.

В нашем исследовании каждый поезд представлен в виде линейной сети со станциями в качестве узлов и дуг, соединяющих обслуживаемые пары станций O-D. Стратегия многоуровневого тарифа создается для удовлетворения спроса каждого O-D. Оптимальная стоимость билета для каждого O-D с течением времени определяется пассажирским спросом, который колеблется в пределах определенного диапазона стандартного тарифа, либо в сторону увеличения, либо в сторону уменьшения. Оставшаяся часть статьи организована следующим образом. В следующем разделе мы представляем модель оптимизации стоимости билетов, основанную на кусочной политике ценообразования. В разделе 3 мы представляем несколько экспериментов и обсуждаем свойства схемы оптимального тарифа, основанной на результатах вычислений. В последнем разделе представлены выводы.

2. Методология

2.1. Постановка задачи и обозначения

В этой статье используются следующие обозначения.

Проблема, которую мы рассматриваем в статье, описывается следующим образом. Железнодорожная компания, работающая на рынке с несовершенной конкуренцией, продает билеты на поезд пассажирам, идущим по разным маршрутам O-D в течение ограниченного временного горизонта (период продажи билетов). До периода продажи билетов количество мест заранее определено и не может быть изменено, а после этого непроданные билеты имеют нулевую ликвидационную стоимость. Одно из решений тактического уровня, которое компания должна принять, — определить количество тарифных категорий и цену каждой категории для каждого O-D, чтобы максимизировать общий доход. Гальего и ван Ризин (1994) [3] показал, что оптимальная цена непрерывно меняется в зависимости от времени до отправления и количества оставшихся мест. Поскольку все время корректировать цену нереально, для практических целей применяется сдельная политика ценообразования, когда в любом интервале периода продажи билетов на О-Д открыт только один тарифный класс.

Транспортная услуга между парой последовательных станций определяется как ресурс , . Транспортная услуга между любой парой станций определяется как продукт, состоящий из одной или нескольких единиц ресурсов. Матрица инцидентности ресурс-продукт представляет собой матрицу 0-1, где ресурс используется продуктом и в противном случае. Начальная вместимость ресурса , количество мест в поезде. Период продажи билетов делится на несколько подпериодов, обозначающих количество подпериодов продукта и обозначающих продолжительность подпериода продукта. Для данного продукта сумма временных отрезков всех подпериодов равна продолжительности периода продажи билетов , который заканчивается, когда поезд отправляется из пункта отправления .

Клиентов обычно делят на две категории: близоруких и стратегических [16]. Стратегические клиенты оптимизируют свое покупательское поведение в соответствии со стратегией ценообразования компании, в то время как близорукие клиенты покупают продукт, как только его цена становится меньше их резервной цены. Чем дороже продукт, тем больше необходимо моделировать стратегических клиентов. Однако у клиентов не так много информации и времени для принятия стратегических решений при покупке железнодорожных билетов. Поэтому мы предполагаем миопическое поведение в этой статье.

Спрос пассажиров обычно характеризуется как процесс Пуассона, для которого спрос в течение определенного периода времени является стохастической переменной. В сетевой формулировке стохастический элемент значительно увеличивает сложность и сложность задачи. Следуя часто используемому методу, мы используем детерминированную модель как аппроксимацию стохастической задачи. Обозначим как плотность спроса (объем спроса в единицу времени) на продукт в подпериод . Согласно гипотезе несовершенной рыночной конкуренции спрос меняется вместе с ценой. Таким образом, плотность спроса описывается как функция времени и цены. Предполагается, что эта функция обладает следующими свойствами. (1) Функция спроса непрерывно дифференцируема и строго убывает с , то есть на допустимом наборе цен. Функция спроса имеет уникальную обратную функцию .(2) Норма дохода равна , которая предполагается непрерывно ограниченной вогнутой.

Примеры включают обычно используемую линейную функцию спроса и экспоненциальную функцию спроса.

2.2. Моделирование

Хотя мы ищем оптимальные цены, удобно использовать функцию плотности спроса , которая является уникальной обратной функцией цены, в качестве переменной решения модели. Тогда модель оптимизации стоимости билета будет следующей:

. Целевая функция (1) состоит в том, чтобы максимизировать общий доход от всех продуктов за весь период продажи билетов. В этой статье мы предполагаем, что билеты продаются в порядке живой очереди. Таким образом, количество принятых запросов на бронирование ограничено только мощностью каждого ресурса, как показано в неравенстве (2). Неравенство (3) ограничивает диапазон, в котором цена колеблется вокруг базовой цены, с верхней границей, основанной на некотором психологическом пороге клиента, и нижней границей транспортных расходов железной дороги. Обозначим базисную цену продукта как , максимальный коэффициент колебаний в сторону понижения как , а максимальный коэффициент колебаний в сторону повышения как .

В соответствии со свойством 2 функции спроса целевая функция модели вогнута, и ограничения также вогнуты. Введя вышеприведенную модель можно преобразовать в выпуклую программу с целью минимизации , для которой точка K-T является оптимальным решением исходной задачи. Модель оптимизации стоимости билета ((1)–(3)) может быть решена путем нахождения точки K-T новой выпуклой программы.

3. Практический пример

3.1. Введение в кейс

Поезд G205 с низким коэффициентом загрузки использовался для проверки нашей стратегии универсального тарифа. Карта маршрута G205 (рис. 1) показывает, что в нашем случае имеется 3 ресурса: Юг-Запад Цзинаня, Запад Цзинань-Восток Сюйчжоу, Восток Сюйчжоу-Нанкин и 6 продуктов: Запад-Юг-Цзинань, Пекин Юг-Сюйчжоу-Восток, Пекин. Юг-Нанкин-Юг, Цзинань-Запад-Сюйчжоу-Восток, Цзинань-Запад-Нанкин-Юг, Сюйчжоу-Восток-Нанкин. Матрица ресурсов-продуктов равна

Поезд G205 имеет пассажировместимость 1005, таким образом, начальная вместимость каждого ресурса , .

Мы используем логарифмическую функцию спроса, обычно используемую в экономике для описания взаимосвязи между спросом и ценой:

В (5) – базисная цена, – плотность спроса при базовой цене, эластичность спроса по цене, отрицательный знак которой означает, что спрос и цена находятся в обратной зависимости. Единственная обратная функция (5), являющаяся выражением цены, равна

Ценовая эластичность спроса является ключевым параметром функции спроса, показывающим степень реакции спроса на изменение цены. Мы оценили ценовую эластичность спроса на O-D поезда G205 по данным о билетах на лето 2013 г. , когда действовали скидки. Эластичность спроса по цене, которая представляет собой отношение процентного изменения спроса и процентного изменения цены, можно рассчитать с помощью следующего уравнения, а полученные оценки показаны в таблице 19.0003

Полученные оценки эластичности спроса по цене согласуются с существующими результатами исследований с точки зрения конкуренции между высокоскоростной железной дорогой и другими видами транспорта [14, 16]. Маршруты O-D Цзинань-Сюйчжоу, Сюйчжоу-Нанкин и Пекин-Цзинань превышают конкурентоспособное расстояние автомобильных перевозок, но меньше, чем у гражданской авиации. Таким образом, чувствительность спроса к цене для этих O-D слаба. Цзинань-Нанкин и Пекин-Сюйчжоу находятся в диапазоне, где гражданская авиация может конкурировать с высокоскоростной железной дорогой, но прямого рейса между этими парами городов нет, что увеличивает время в пути и сложность авиасообщения. Поскольку авиаперевозки дороже высокоскоростных поездов, пассажиры в основном выбирают высокоскоростные поезда, а чувствительность спроса к цене остается слабой для двух O-D. Для сравнения, путь от Пекина до Нанкина находится на расстоянии, на котором конкурируют высокоскоростная железная дорога и гражданская авиация, а между городами есть прямые рейсы. Поскольку у пассажиров есть конкурирующие варианты поездок, спрос более чувствителен к цене.

3.2. Результаты вычислений

Мы применяем MATLAB для решения предложенной выше задачи оптимизации стоимости билета. Проводятся два эксперимента для изучения характеристик оптимальной схемы оплаты проезда. Первый исследует взаимосвязь между оптимальной схемой оплаты проезда и ценовой эластичностью спроса.

Мы анализируем регулярность прибытия пассажиров в качестве основы для первого эксперимента, используя исторические данные о билетах на высокоскоростную железную дорогу Пекин-Шанхай в период с 1 марта 2013 г. по 13 марта 2014 г. Для определенного поезда обозначает плотность спроса в час для O-D в день. Это значение количества билетов, проданных за O-D в день, деленное на количество часов продажи билетов в этот день. Отношение плотности спроса O-D в день (количество дней периода продажи билетов) указывает на интенсивность спроса в день. Усреднение стоимости всех поездов для дает коэффициент плотности ежедневного спроса по O-D. На рис. 2 показаны эти результаты.

Как показано на рисунке 2, коэффициент плотности спроса увеличивается со временем, за исключением первого дня и дня отъезда. В первом эксперименте мы разделяем период продажи билетов на два сегмента, где коэффициент плотности спроса равен 5 процентам. Для данного O-D первый подпериод начинается с первого дня до последнего дня с коэффициентом плотности спроса меньше или равным 5%, а остальные дни относятся ко второму подпериоду. В соответствии с этим методом предлагаются два уровня тарифа, при этом каждый подпериод имеет одну цену. В качестве базовой цены используется текущая цена билета, вокруг которой устанавливается максимальный процент колебания в сторону понижения, а максимальный процент колебания в сторону увеличения составляет . В таблице 2 представлены параметры эксперимента, включая количество часов продажи билетов в течение каждого подпериода , почасовую плотность спроса при базовой цене и базовой цене .

Обычно считается, что туристы, чувствительные к цене, обычно прибывают раньше, тогда как деловые путешественники, которые не так чувствительны к цене, прибывают поздно. В соответствии с этой гипотезой мы установили ценовую эластичность спроса первого подпериода на 10% выше, чем эластичность спроса второго подпериода. Ценовая эластичность спроса, рассчитанная на основе исторических данных о билетах (см. Таблицу 1), которая считается равной 1, представляет собой среднее значение двух подпериодов. Мы постепенно увеличиваем среднюю ценовую эластичность на 10% и получаем доход от поезда и коэффициент загрузки оптимальной тарифной схемы на каждом уровне ценовой эластичности спроса. На рис. 3 показаны результаты.

Мы видим, что доход от поездов и коэффициент загрузки увеличиваются с эластичностью спроса по цене, что указывает на то, что чем более чувствителен спрос к цене, тем лучше эффект от применения стратегии многоуровневого тарифа. Это важно на рынке с множеством конкурирующих видов транспорта.

Второй эксперимент исследует взаимосвязь между оптимальной схемой оплаты проезда и количеством тарифных категорий. Определяем оптимальные тарифные схемы для двух, трех и четырех классов тарифов, а также выручку и загрузку поезда. В таблице 3 представлены эти результаты вместе с базовой схемой тарифов.

Таблица 3 показывает, что доход от поезда увеличивается с увеличением количества тарифов, хотя процент увеличения коэффициента загрузки снижается по сравнению с базовым тарифом. Поскольку китайский железнодорожный транспорт служит общественному благосостоянию, мы должны стремиться к получению прибыли, максимально удовлетворяя потребности пассажиров в поездках. Таким образом, стратегия трехуровневого тарифа, которая уравновешивает доход от поезда и коэффициент загрузки, является наиболее подходящей. В таблице 4 представлены входные параметры и оптимальное решение для трехуровневой тарифной стратегии.

Эксперименты, в которых используются фактические данные, показывают, что стратегия многоуровневого тарифа может не только увеличить доход, но и стимулировать потенциальный спрос по сравнению с существующей структурой единого тарифа. Это указывает на то, что стратегия многоуровневого тарифа подходит для высокоскоростной железной дороги Китая, особенно на рынке с жесткой конкуренцией с другими видами транспорта. Второй эксперимент говорит о том, что количество тарифных разрядов не должно быть слишком большим, что также было подтверждено на практике опытом железных дорог Великобритании и Франции [17].

4. Выводы

В этом документе исследуется применение многоуровневой структуры тарифа в HSR Китая, где всегда использовалась стратегия одноуровневого тарифа. Наша цель — максимизировать ожидаемый доход от поезда, установив несколько цен на билеты в соответствии с различными оценками пассажиров.

На основе стратегии кусочного ценообразования мы сначала строим модель оптимизации стоимости билетов, которую можно преобразовать в выпуклую программу для решения. Взяв в качестве примера поезд G205, мы провели два эксперимента для изучения свойств оптимальной схемы оплаты проезда. Результаты эксперимента показывают, что чем более чувствителен спрос к цене, тем лучше эффект применения стратегии универсального тарифа. Сравнивая оптимальные решения различных тарифных схем с базовой тарифной стратегией, мы обнаруживаем, что многоуровневая тарифная стратегия может увеличить как доход от поезда, так и коэффициент загрузки. Это указывает на то, что универсальный тариф подходит для высокоскоростной железной дороги Китая. Наконец, мы даем предложение по определению наиболее подходящей схемы многоуровневого тарифа. Поскольку китайская железная дорога является полунекоммерческой организацией, которая должна преследовать цель максимально удовлетворить потребности пассажиров в поездках, мы рекомендуем трехуровневую схему оплаты проезда, которая уравновешивает доходы от поездов и коэффициент загрузки.

Безусловно, в этой области существует множество возможных направлений будущих исследований. В этой статье предполагается, что поведение пассажиров является детерминированным, а величина спроса фиксированной. Если быть более реалистичным, то в будущих исследованиях следует учитывать реакцию пассажиров на оптимизацию стоимости билетов, а величину спроса следует считать эластичной. Другое направление — расширить наше исследование на систему с несколькими поездами. Поскольку корректировка стоимости билета на какой-либо поезд приведет к пересадке пассажиров между поездами, которые предоставляют ту же транспортную услугу O-D, нам следует дополнительно изучить, как совместно оптимизировать стоимость билетов на эти поезда.

Notations

:	Symbol of source,
:	Symbol of product,
:	Initial capacity of resource
:	Demand density of product in subperiod
:	Продолжительность субпериода продукта
:	Цена продукта в субпериоде
: 909152	0152
:	Basis price of product
:	The number of ticket-selling subperiods
:	Resource-product incidence matrix
:	Maximum downward fluctuation ratio of price
:	Максимальный коэффициент восходящего колебания цены.

Конкурирующие интересы

Авторы заявляют, что у них нет конкурирующих интересов.

Благодарности

Это исследование было проведено при поддержке проекта плана технологических исследований и разработок Китайской железнодорожной корпорации (2016X005-E).

Ссылки

И. Л. Гейл и Т. Дж. Холмс, «Эффективность скидок на предварительную покупку в условиях неопределенности совокупного спроса», International Journal of Industrial Organization , vol. 10, нет. 3, стр. 413–437, 1992.
Посмотреть по адресу:
Сайт издателя | Академия Google
У. М. Кинкейд и Д. А. Дарлинг, «Проблема ценообразования запасов», Journal of Mathematical Analysis and Applications , vol. 7, стр. 183–208, 1963.
Посмотреть по адресу:
Сайт издателя | ученый Google | Zentralblatt МАТЕМАТИКА | MathSciNet
Г. Гальего и Г. ван Райзин, «Оптимальное динамическое ценообразование запасов со стохастическим спросом на конечных горизонтах», Management Science , vol. 40, нет. 8, стр. 999–1020, 1994.
Посмотреть по адресу:
Сайт издателя | ученый Google | Zentralblatt MATH
G. Gallego и G. Van Ryzin, «Проблема динамического ценообразования для нескольких продуктов и ее приложения к управлению доходностью сети», Operations Research , vol. 45, нет. 1, стр. 24–41, 1997.
Посмотреть по адресу:
Сайт издателя | ученый Google | Zentralblatt MATH
Y. Feng и G. Gallego, «Оптимальное время начала продаж в конце сезона и оптимальное время остановки для рекламных тарифов», Наука управления , том. 41, нет. 8, стр. 1371–1391, 1995.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю. Фэн и Б. Сяо, «Оптимальные политики управления доходностью с несколькими заранее определенными ценами», Operations Research , vol. 48, нет. 2, стр. 332–343, 2000.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю. Фэн и Б. Сяо, «Модель непрерывного управления доходностью с несколькими ценами и обратимыми изменениями цен», Наука управления , том. 46, нет. 5, стр. 644–657, 2000.
Посмотреть по адресу:
Сайт издателя | ученый Google | Zentralblatt MATH
Ф. Ши, «Оптимальное динамическое ценообразование на железнодорожный пассажирский билет», Журнал Китайского железнодорожного общества , том. 24, нет. 1, pp. 1–4, 2002.
Посмотреть по адресу:
Google Scholar
X. Zhang, Исследование продаж железнодорожных билетов со скидкой в Китае , Southwest Jiaotong University, Chengdu, China, 2005.
Z. Xu, L. Weixin, C. Quande и Z. Bingru, «Исследование динамического ценообразования между высокоскоростным железнодорожным и воздушным транспортом под влиянием индуцированного пассажиропотока», Information Technology Journal , vol. 11, нет. 4, стр. 431–435, 2012 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
E. Yao, Q. Yang, Y. Zhang и X. Sun, «Исследование стратегии ценообразования на высокоскоростных железных дорогах в контексте конкуренции видов транспорта», Discrete Dynamics in Nature and Society , том. 2013 г., идентификатор статьи 715256, 6 страниц, 2013 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Q. Bingyi, Исследование управления доходами для выделенных пассажирских линий на основе поведения пассажиров , Southwest Jiaotong Universiy, Chengdu, China, 2014.
L. Chen, J. Wei, H. H. Цзян, Х. Ван и Х. Шао, «Исследование модели двухуровневого программирования тарифов на высокоскоростные железные дороги на основе обобщенной функции затрат», Journal of Railway Science and Engineering , том. 12, нет. 2, стр. 250–256, 2015 г.
Посмотреть по адресу:
Google Scholar
В. Ли и З. Фу, «Анализ эластичности спроса на высокоскоростные железнодорожные пассажирские перевозки», Journal of Railway Science and Машиностроение , вып. 13, нет. 11, стр. 2115–2124, 2016.
Просмотр по адресу:
Google Scholar
Дж. Чжэн и Дж. Лю, «Исследование оптимизации стоимости билетов для высокоскоростных поездов Китая», Математические проблемы в Инжиниринг , том. 2016 г., идентификатор статьи 5073053, 8 страниц, 2016 г.
Посмотреть по адресу:
Сайт издателя | ученый Google | MathSciNet
К.